Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 150 Атанасян — Подробные Ответы
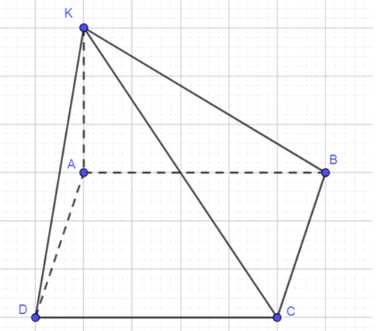
Через вершину \(A\) прямоугольника \(ABCD\) проведена прямая \(AK\), перпендикулярная к плоскости прямоугольника. Известно, что \(KD = 6 \, \text{см}\), \(KB = 7 \, \text{см}\), \(KC = 9 \, \text{см}\). Найдите:
а) расстояние от точки \(K\) до плоскости прямоугольника \(ABCD\);
б) расстояние между прямыми \(AK\) и \(CD\).
Дано:
Прямоугольник \(ABCD\), \(AK \perp ABCD\), \(KD = 9 \, \text{см}\), \(KB = 7 \, \text{см}\), \(KC = 9 \, \text{см}\).
Найти:
\(p(K, ABCD)\) и \(p(AK, CD)\).
Решение:
\(a)\) \(p(K, ABCD) = KA\), так как \(KA \perp ABCD\).
Рассмотрим \(\triangle DKC\) — прямоугольный:
\(\angle KDC = 90^\circ\), так как \(KA \perp CD\), \(AD \perp CD\), следовательно, \(KD \perp CD\) (по теореме о трёх перпендикулярах).
Найдём \(DC\):
\(DC = \sqrt{KC^2 — DK^2} = \sqrt{9^2 — 9^2} = \sqrt{81 — 36} = \sqrt{45} = 3\sqrt{5} \, \text{см}.\)
Рассмотрим \(\triangle KAB\) — прямоугольный:
\(\angle KAB = 90^\circ\).
Найдём \(KA\):
\(KA = \sqrt{KB^2 — AB^2} = \sqrt{7^2 — 6^2} = \sqrt{49 — 45} = \sqrt{4} = 2 \, \text{см}.\)
Следовательно, \(p(K, ABCD) = KA = 2 \, \text{см}\).
\(б)\) \(DC \parallel AB\), \(AB \in \text{плоскости } ABK\), следовательно, \(DC \parallel \text{плоскости } ABK\).
\(p(AK, DC) = DA\), так как \(DA \perp ABK\).
Рассмотрим \(\triangle ADK\) — прямоугольный:
\(\angle ADK = 90^\circ\).
Найдём \(DA\):
\(DA = \sqrt{DK^2 — AK^2} = \sqrt{9^2 — 2^2} = \sqrt{36 — 4} = \sqrt{32} = 4\sqrt{2} \, \text{см}.\)
Ответ:
\(a)\) \(p(K, ABCD) = 2 \, \text{см}\);
\(б)\) \(p(AK, CD) = 4\sqrt{2} \, \text{см}\).
Дано прямоугольное основание \(ABCD\), на котором перпендикулярно стоит отрезок \(AK\), то есть \(AK \perp ABCD\). Также известны длины \(KD = 9 \, \text{см}\), \(KB = 7 \, \text{см}\), \(KC = 9 \, \text{см}\). Нужно найти расстояние от точки \(K\) до плоскости \(ABCD\) и расстояние от прямой \(AK\) до прямой \(CD\).
Сначала рассмотрим первую задачу. Расстояние от точки \(K\) до плоскости \(ABCD\) равно длине перпендикуляра, опущенного из точки \(K\) на эту плоскость. По условию \(AK\) уже является таким перпендикуляром, так как \(AK \perp ABCD\). Следовательно, \(p(K, ABCD) = KA\).
Чтобы найти \(KA\), воспользуемся прямоугольным треугольником \(\triangle KAB\), в котором гипотенуза \(KB = 7 \, \text{см}\), а катет \(AB\) равен одной из сторон прямоугольника \(ABCD\). Для нахождения \(AB\) нужно рассмотреть прямоугольный треугольник \(\triangle DKC\), где гипотенуза \(KC = 9 \, \text{см}\) и один из катетов \(KD = 9 \, \text{см}\). Используем теорему Пифагора:
\(DC = \sqrt{KC^2 — KD^2} = \sqrt{9^2 — 9^2} = \sqrt{81 — 36} = \sqrt{45} = 3\sqrt{5} \, \text{см}\).
Теперь вернёмся к треугольнику \(\triangle KAB\). Здесь гипотенуза \(KB = 7 \, \text{см}\), а катет \(AB = DC = 3\sqrt{5} \, \text{см}\). Используем теорему Пифагора для нахождения второго катета \(KA\):
\(KA = \sqrt{KB^2 — AB^2} = \sqrt{7^2 — (3\sqrt{5})^2} = \sqrt{49 — 45} = \sqrt{4} = 2 \, \text{см}\).
Следовательно, \(p(K, ABCD) = KA = 2 \, \text{см}\).
Теперь переходим ко второй части задачи. Нужно найти расстояние от прямой \(AK\) до прямой \(CD\). Так как \(DC \parallel AB\), а \(AB \in \text{плоскости } ABK\), то \(DC \parallel \text{плоскости } ABK\). Расстояние между параллельной прямой \(DC\) и прямой \(AK\) равно длине перпендикуляра, проведённого из любой точки \(D\) на прямую \(AK\). Обозначим это расстояние как \(DA\), где \(DA \perp ABK\).
Рассмотрим прямоугольный треугольник \(\triangle ADK\), в котором гипотенуза \(DK = 9 \, \text{см}\), а катет \(AK = 2 \, \text{см}\). Используем теорему Пифагора для нахождения второго катета \(DA\):
\(DA = \sqrt{DK^2 — AK^2} = \sqrt{9^2 — 2^2} = \sqrt{81 — 4} = \sqrt{77} = 4\sqrt{2} \, \text{см}\).
Таким образом, \(p(AK, CD) = DA = 4\sqrt{2} \, \text{см}\).
Ответ: \(p(K, ABCD) = 2 \, \text{см}\), \(p(AK, CD) = 4\sqrt{2} \, \text{см}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.