
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 146 Атанасян — Подробные Ответы
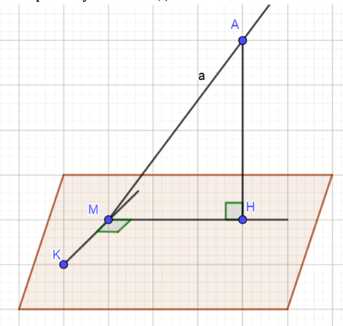
Прямая \(a\) пересекает плоскость \(\sigma\) в точке \(M\) и не перпендикулярна к этой плоскости. Докажите, что в плоскости \(\sigma\) через точку \(M\) проходит прямая, перпендикулярная к прямой \(a\), и притом только одна.
Дано: \( a \cap \alpha = M \); \( a \perp \alpha \).
Доказать: В плоскости \(\alpha\) через точку \(M\) проходит прямая \(l \perp a\), и притом только одна.
Доказательство:
Из точки \(A \in a\) опустим перпендикуляр \(AH\) на \(\alpha\) (по теореме п. 18 он существует и притом только один).
Проведем прямую \(MH\).
В плоскости \(\alpha\) через точку \(M\) проходит прямая, перпендикулярная \(MH\), и притом только одна (курс планиметрии). Обозначим эту прямую \(MK\) (\(MK \perp MH\)).
\(AM\) — наклонная, \(MH\) — проекция, \(MK \perp MH\), следовательно, по теореме о трёх перпендикулярах \(AM \perp MK\), а так как \(AM \in \alpha\), то и \(\alpha \perp MK\).
\(MK \perp MH\) и \(MK \perp AM\), значит, \(MK \perp \triangle AMH\).
Предположим, что в плоскости \(\alpha\) существует ещё одна прямая \(MQ \perp a\). Тогда \(MQ \perp \triangle AMH\) (так как \(MQ \perp AM \Rightarrow MQ \perp MH\)), но через точку \(M\) уже проходит прямая \(MK \perp \triangle AMH\). Однако по теореме п. 18 такая прямая существует только одна, следовательно, \(MK = MQ\).
Таким образом, в плоскости \(\alpha\) существует прямая, проходящая через точку \(M\) и перпендикулярная \(a\), и притом только одна, что и требовалось доказать.
Дано условие: \(a \cap \alpha = M\), \(a \perp \alpha\). Требуется доказать, что в плоскости \(\alpha\) через точку \(M\) проходит прямая \(l \perp a\), причём такая прямая только одна.
Для доказательства сначала из точки \(A \in a\) опустим перпендикуляр \(AH\) на плоскость \(\alpha\). Согласно теореме из стереометрии (теорема п. 18), такой перпендикуляр существует и притом только один. Это важно, так как \(AH\) задаёт направление, связанное с плоскостью \(\alpha\), и позволяет нам рассматривать проекции и наклонные относительно этой плоскости.
Далее проведём прямую \(MH\), соединяющую точку пересечения \(M\) и основание перпендикуляра \(H\). Прямая \(MH\) лежит в плоскости \(\alpha\), так как обе её точки \(M\) и \(H\) принадлежат \(\alpha\).
Теперь в плоскости \(\alpha\) через точку \(M\) можно провести прямую, которая будет перпендикулярна \(MH\). Согласно курсу планиметрии, такая прямая существует и притом только одна. Обозначим эту прямую как \(MK\), причём \(MK \perp MH\). Это ключевой шаг, так как \(MK\) задаёт направление, которое перпендикулярно проекции \(MH\) в плоскости \(\alpha\).
Рассмотрим наклонную \(AM\), проведённую из точки \(A \in a\) к точке \(M\). Прямая \(MH\) является проекцией наклонной \(AM\) на плоскость \(\alpha\). Так как \(MK \perp MH\), то, по теореме о трёх перпендикулярах, наклонная \(AM\) перпендикулярна прямой \(MK\). Поскольку \(AM \in a\), а \(a \perp \alpha\), то и вся плоскость \(\alpha\) перпендикулярна \(MK\). Это означает, что \(MK \perp a\).
Далее предположим, что в плоскости \(\alpha\) существует ещё одна прямая \(MQ\), которая также перпендикулярна \(a\). Тогда прямая \(MQ\) будет перпендикулярна треугольнику \(AMH\), так как \(MQ \perp AM\) и \(MQ \perp MH\). Однако через точку \(M\) уже проходит прямая \(MK\), которая перпендикулярна \(AMH\). Согласно теореме п. 18, такая прямая, проходящая через точку \(M\) и перпендикулярная плоскости \(\alpha\), может быть только одна. Следовательно, \(MQ = MK\).
Таким образом, в плоскости \(\alpha\) через точку \(M\) существует единственная прямая \(MK\), которая перпендикулярна \(a\). Это завершает доказательство.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!