ГДЗ по Геометрии 10 класс Номер 144 Атанасян — Подробные Ответы

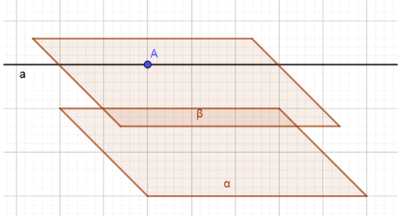
Прямая \(a\) параллельна плоскости \(\sigma\). Докажите, что все точки прямой \(a\) равноудалены от плоскости \(\sigma\).

Решение:
Через какую-нибудь точку прямой \(a\) проведём плоскость \(\beta\), параллельную плоскости \(\sigma\) (задача 59). Прямая \(a\) лежит в плоскости \(\beta\), так как в противном случае она пересекала бы плоскость \(\beta\), а значит, пересекала бы и плоскость \(\sigma\) (задача 55), что невозможно. Все точки плоскости \(\beta\) равноудалены от плоскости \(\sigma\), поэтому и все точки прямой \(a\), лежащей в плоскости \(\beta\), равноудалены от плоскости \(\sigma\), что и требовалось доказать.

Дано: \(a \parallel \alpha\).
Доказать: все точки \(a\) равноудалены от \(\alpha\).

Доказательство:
Отметим какую-либо точку \(A\) на прямой \(a\).

Через точку \(A\) проведем плоскость \(\beta\), такую что \(\beta \parallel \alpha\).

Поскольку \(a \subset \beta\), то прямая \(a\) лежит в плоскости \(\beta\). Если бы это было не так, то \(a\) пересекала бы \(\beta\), а это, в свою очередь, означало бы пересечение прямой \(a\) с плоскостью \(\alpha\), что противоречит условию \(a \parallel \alpha\).

Таким образом, все точки плоскости \(\beta\) равноудалены от плоскости \(\alpha\), так как \(\beta \parallel \alpha\).

Следовательно, все точки прямой \(a\), лежащей в плоскости \(\beta\), также равноудалены от плоскости \(\alpha\), что и требовалось доказать.

Дано условие, что прямая \(a\) параллельна плоскости \(\alpha\), то есть \(a \parallel \alpha\). Необходимо доказать, что все точки прямой \(a\) равноудалены от плоскости \(\alpha\).

Для доказательства начнем с выбора произвольной точки \(A\) на прямой \(a\). Это допустимо, так как любая прямая состоит из множества точек, и точка \(A\) является одной из них.

Через точку \(A\) проведем плоскость \(\beta\), которая параллельна плоскости \(\alpha\), то есть \(\beta \parallel \alpha\). Это можно сделать, так как для любой точки пространства существует единственная плоскость, проходящая через эту точку и параллельная заданной плоскости.

Далее заметим, что прямая \(a\) лежит в плоскости \(\beta\). Это следует из того, что точка \(A\), принадлежащая прямой \(a\), является общей точкой \(a\) и \(\beta\). Если бы прямая \(a\) не лежала в \(\beta\), то она пересекала бы \(\beta\), а это, в свою очередь, привело бы к пересечению \(a\) с плоскостью \(\alpha\), что невозможно, так как \(a \parallel \alpha\). Таким образом, \(a \subset \beta\).

Теперь, зная, что \(\beta \parallel \alpha\), мы можем утверждать, что все точки плоскости \(\beta\) равноудалены от плоскости \(\alpha\). Это свойство параллельных плоскостей: расстояние между ними остается постоянным.

Так как прямая \(a\) полностью лежит в плоскости \(\beta\), то все точки прямой \(a\) также равноудалены от плоскости \(\alpha\). Это следует из того, что расстояние от любой точки \(a\) до \(\alpha\) равно расстоянию от соответствующей точки \(\beta\) до \(\alpha\).

Таким образом, мы доказали, что все точки прямой \(a\) равноудалены от плоскости \(\alpha\), что и требовалось показать.