
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 142 Атанасян — Подробные Ответы
Концы отрезка отстоят от плоскости \(\sigma\) на расстояниях \(1 \, \text{см}\) и \(4 \, \text{см}\). Найдите расстояние от середины отрезка до плоскости \(\sigma\).
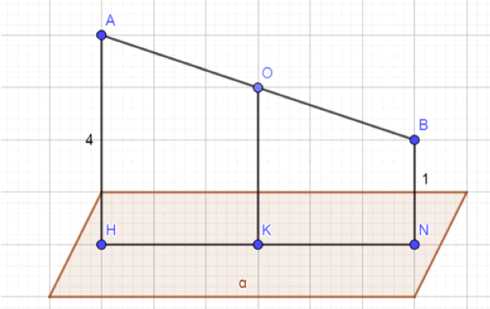
Доказательство, что \(ABNH\) — трапеция:
Из условия \(AH \perp a\) и \(BN \perp a\). Если два отрезка перпендикулярны одной прямой, то они параллельны. Следовательно, \(AH \parallel BN\), а значит, \(ABNH\) — трапеция.
Средняя линия трапеции \(OK\):
Средняя линия равна полусумме оснований:
\(
OK = \frac{1}{2} (AH + BN).
\)
Подставим \(AH = 4 \, \text{см}\) и \(BN = 1 \, \text{см}\):
\(
OK = \frac{1}{2} (4 + 1) = \frac{5}{2} = 2,5 \, \text{см}.
\)
Подобие треугольников \(\triangle AMH\) и \(\triangle BMN\):
Из \(AH \parallel BN\) углы \(\angle AMH = \angle BMN\), \(\angle MAH = \angle MBN\). Значит, \(\triangle AMH \sim \triangle BMN\). Отношение сторон:
\(
\frac{BM}{AM} = \frac{BN}{AH}.
\)
Подставим \(BN = 1 \, \text{см}\), \(AH = 4 \, \text{см}\):
\(
\frac{BM}{AM} = \frac{1}{4}.
\)
Так как \(AB = AM + BM\), то \(AB = 5BM\).
Подобие треугольников \(\triangle OMK\) и \(\triangle BMN\):
Из \(OK \parallel BN\) углы \(\angle OMK = \angle BMN\), \(\angle MOK = \angle MBN\). Значит, \(\triangle OMK \sim \triangle BMN\). Отношение сторон:
\(
\frac{OK}{BN} = \frac{OM}{BM}.
\)
По условию \(BO = \frac{5}{2} BM\), тогда
\(
OM = BO — BM = \frac{5}{2} BM — BM = \frac{3}{2} BM.
\)
Подставим:
\(
\frac{OK}{BN} = \frac{\frac{3}{2} BM}{BM}.
\)
Сократим \(BM\):
\(
\frac{OK}{BN} = \frac{3}{2}.
\)
Подставим \(BN = 1 \, \text{см}\):
\(
OK = \frac{3}{2} = 1,5 \, \text{см}.
\)
Ответ:
\((a) \, OK = 3 \, \text{см}; \, (б) \, OK = 1,5 \, \text{см}.\)
Дано:
\(AH = 4 \, \text{см}; \, BN = 1 \, \text{см}; \, HK = KN; \, AO = OB; \, AB \parallel a = M\).
Найти: \(OK — ?\).
Рассуждение:
В пункте (a) сначала нужно доказать, что \(ABNH\) является трапецией. Для этого проверим, что \(AH \parallel BN\). Из условия известно, что \(AH \perp a\) и \(BN \perp a\). Если два отрезка перпендикулярны одной и той же прямой, то они параллельны между собой. Следовательно, \(AH \parallel BN\), а значит, \(ABNH\) — трапеция.
Далее рассмотрим среднюю линию трапеции \(ABNH\). Средняя линия трапеции — это отрезок, который соединяет середины её боковых сторон и параллелен основаниям трапеции. Из условия известно, что \(O\) — середина \(AB\), а \(OK \perp a\) и \(AH \perp a\). Это означает, что \(OK \parallel AH \parallel BN\), и \(OK\) является средней линией трапеции \(ABNH\).
Средняя линия трапеции равна полусумме её оснований. Таким образом, для нахождения длины \(OK\) используем формулу:
\(OK = \frac{1}{2} (AH + BN)\).
Подставим значения \(AH = 4 \, \text{см}\) и \(BN = 1 \, \text{см}\):
\(OK = \frac{1}{2} (4 + 1) = \frac{5}{2} = 2,5 \, \text{см}\).
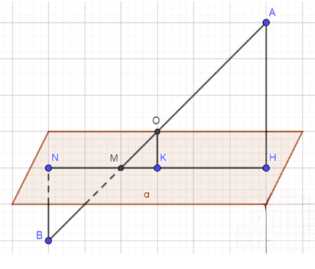
В пункте (б) сначала докажем подобие треугольников \(\triangle AMH\) и \(\triangle BMN\). Из условия \(AH \parallel BN\), а значит, углы \(\angle AMH\) и \(\angle BMN\) равны как вертикальные. Углы \(\angle MAH\) и \(\angle MBN\) равны как накрестлежащие при пересечении секущей \(AB\) с параллельными прямыми \(AH\) и \(BN\). Следовательно, треугольники \(\triangle AMH\) и \(\triangle BMN\) подобны по двум углам.
Из подобия треугольников следует, что отношения соответствующих сторон пропорциональны. Таким образом,
\((BM : AM) = (BN : AH)\).
Подставим значения \(BN = 1 \, \text{см}\) и \(AH = 4 \, \text{см}\):
\(BM : AM = 1 : 4\).
Так как \(AB = AM + BM\), то \(AB : BM = 5 : 1\), откуда \(AB = 5BM\).
Теперь рассмотрим треугольники \(\triangle OMK\) и \(\triangle BMN\). Из условия \(OK \parallel BN\), а значит, углы \(\angle OMK\) и \(\angle BMN\) равны как вертикальные. Углы \(\angle MOK\) и \(\angle MBN\) равны как накрестлежащие при пересечении секущей \(AB\) с параллельными прямыми \(OK\) и \(BN\). Следовательно, треугольники \(\triangle OMK\) и \(\triangle BMN\) подобны по двум углам.
Из подобия треугольников следует, что
\((OK : BN) = (OM : BM)\).
По условию \(BO = \frac{5}{2} BM\). Тогда
\(OM = BO — BM = \frac{5}{2} BM — BM = \frac{3}{2} BM\).
Подставим это в пропорцию:
\((OK : BN) = (\frac{3}{2} BM : BM)\).
Сократим \(BM\):
\(OK : BN = \frac{3}{2}\).
Подставим \(BN = 1 \, \text{см}\):
\(OK : 1 = \frac{3}{2}\), откуда \(OK = 1,5 \, \text{см}\).
Ответ:
\(a) \, OK = 3 \, \text{см}; \, б) \, OK = 1,5 \, \text{см}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!