
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 141 Атанасян — Подробные Ответы
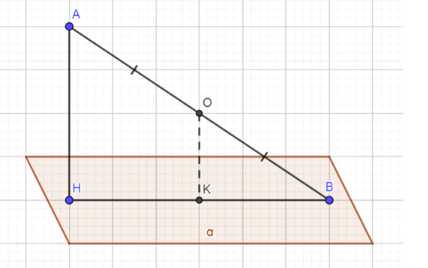
Один конец данного отрезка лежит в плоскости \(\sigma\), а другой находится от неё на расстоянии \(6 \, \text{см}\). Найдите расстояние от середины данного отрезка до плоскости \(\sigma\).
Дано:
\(A \in \alpha\), \(B \in \alpha\);
\(AH = 6 \, \text{см}\);
\(AO = OB\).
Найти:
\(OK = ?\).
Решение:
\(AH\) — это расстояние от точки \(A\) до плоскости \(\alpha\), следовательно, \(AH \perp \alpha\).
\(OK\) — это расстояние от точки \(O\) до плоскости \(\alpha\), следовательно, \(OK \perp \alpha\).
Так как \(AH \perp \alpha\) и \(OK \perp \alpha\), то \(AH \parallel OK\).
Рассмотрим четырёхугольник \(\triangle ABH\):
Из условия \(AH \parallel OK\) и \(AO = OB\), следовательно, \(OK\) является средней линией \(\triangle ABH\).
По свойству средней линии:
\(
OK = \frac{1}{2} \cdot AH.
\)
Подставим значение \(AH = 6 \, \text{см}\):
\(
OK = \frac{1}{2} \cdot 6 = 3 \, \text{см}.
\)
Ответ:
\(OK = 3 \, \text{см}\).
Дано: \(A \in \alpha\), \(B \in \alpha\); \(AH = 6 \, \text{см}\); \(AO = OB\). Нужно найти \(OK\).
Рассмотрим, что \(AH\) и \(OK\) представляют собой расстояния от точек \(A\) и \(O\) до плоскости \(\alpha\). Это означает, что \(AH\) и \(OK\) перпендикулярны плоскости \(\alpha\), то есть \(AH \perp \alpha\) и \(OK \perp \alpha\).
Так как обе линии \(AH\) и \(OK\) перпендикулярны одной и той же плоскости \(\alpha\), то они параллельны друг другу, то есть \(AH \parallel OK\).
Теперь рассмотрим треугольник \(\triangle ABH\). Из условия задачи известно, что \(AO = OB\), что означает, что точка \(O\) является серединой отрезка \(AB\). Таким образом, если рассмотреть отрезок \(OK\), то он будет средней линией треугольника \(\triangle ABH\).
Согласно свойству средней линии треугольника, длина средней линии равна половине длины стороны, параллельной этой средней линии. В данном случае, средней линией является \(OK\), а параллельной стороной — \(AH\).
Таким образом, можем записать:
\(OK = \frac{1}{2} \cdot AH\).
Подставляя известное значение \(AH = 6 \, \text{см}\), получаем:
\(OK = \frac{1}{2} \cdot 6 = 3 \, \text{см}\).
Следовательно, длина \(OK\) равна 3 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!