Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 140 Атанасян — Подробные Ответы
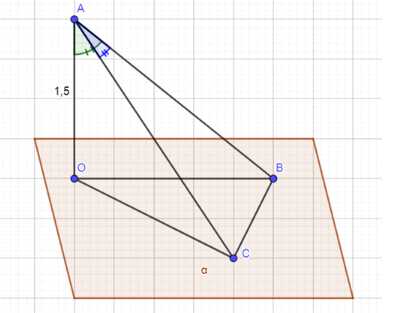
Из точки \(A\), не принадлежащей плоскости \(\sigma\), проведены к этой плоскости перпендикуляр \(AO\) и две равные наклонные \(AB\) и \(AC\). Известно, что \(\angle OAB = \angle BAC = 60^\circ\), \(AO = 1.5 \, \text{см}\). Найдите расстояние между основаниями наклонных.
Дано:
\( A \in \alpha; \, AO \perp \alpha; \, AB = AC \) — наклонные;
\(\angle OAB = \angle BAC = 60^\circ\);
\( AO = 1.5 \, \text{см} \).
Найти:
\( BC = ? \).
Решение:
Рассмотрим треугольник \( \triangle AOB \), который является прямоугольным (так как \( AO \perp AB \)).
Сумма углов в треугольнике равна \( 180^\circ \), тогда:
\(
\angle OBA = 180^\circ — 90^\circ — 60^\circ = 30^\circ.
\)
В прямоугольном треугольнике \( \triangle AOB \) катет \( AO \) и гипотенуза \( AB \) связаны соотношением:
\(
AO = \frac{1}{2} AB.
\)
Отсюда:
\(
AB = 2 \cdot AO = 2 \cdot 1.5 = 3 \, \text{см}.
\)
Теперь рассмотрим треугольник \( \triangle ABC \).
По условию \( CA = AB \) и \(\angle A = 60^\circ\), значит, треугольник \( \triangle ABC \) является равнобедренным.
В равнобедренном треугольнике углы при основании равны. Тогда:
\(
\angle B = \angle C = \frac{180^\circ — \angle A}{2} = \frac{180^\circ — 60^\circ}{2} = 60^\circ.
\)
Таким образом, \( \triangle ABC \) оказывается равносторонним, и все его стороны равны:
\(
BC = AB = 3 \, \text{см}.
\)
Ответ:
\(
BC = 3 \, \text{см}.
\)
Дано: точка \( A \) лежит на плоскости \( \alpha \), прямая \( AO \) перпендикулярна этой плоскости. Отрезки \( AB \) и \( AC \) представляют собой наклонные, которые выходят из точки \( A \). Углы \( \angle OAB \) и \( \angle BAC \) равны \( 60^\circ \). Длина отрезка \( AO \) равна \( 1.5 \, \text{см} \). Необходимо найти длину отрезка \( BC \).
Рассмотрим треугольник \( \triangle AOB \). Этот треугольник является прямоугольным, так как \( AO \perp AB \). В прямоугольном треугольнике сумма углов равна \( 180^\circ \). Один из углов, \( \angle OAB \), равен \( 60^\circ \), а \( \angle AOB \) равен \( 90^\circ \), так как угол между высотой и наклонной всегда прямой. Тогда третий угол \( \angle OBA \) находится по формуле:
\(
\angle OBA = 180^\circ — \angle AOB — \angle OAB = 180^\circ — 90^\circ — 60^\circ = 30^\circ
\).
В прямоугольном треугольнике \( \triangle AOB \) катет \( AO \) и гипотенуза \( AB \) связаны соотношением для угла \( 30^\circ \). Согласно свойствам прямоугольного треугольника, катет, лежащий напротив угла \( 30^\circ \), равен половине гипотенузы. То есть:
\(
AO = \frac{1}{2} AB
\).
Подставим известное значение \( AO = 1.5 \, \text{см} \):
\(
1.5 = \frac{1}{2} AB
\).
Умножим обе части уравнения на 2, чтобы найти \( AB \):
\(
AB = 2 \cdot 1.5 = 3 \, \text{см}
\).
Теперь рассмотрим треугольник \( \triangle ABC \). По условию \( AB = AC \), а угол \( \angle BAC \) равен \( 60^\circ \). Это означает, что треугольник \( \triangle ABC \) является равнобедренным. В любом равнобедренном треугольнике углы при основании равны. Найдем углы \( \angle ABC \) и \( \angle ACB \). Сумма углов треугольника равна \( 180^\circ \), поэтому:
\(
\angle ABC = \angle ACB = \frac{180^\circ — \angle BAC}{2} = \frac{180^\circ — 60^\circ}{2} = 60^\circ
\).
Таким образом, все углы треугольника \( \triangle ABC \) равны \( 60^\circ \), что делает его равносторонним. В равностороннем треугольнике все стороны равны, поэтому:
\(
BC = AB = AC = 3 \, \text{см}
\).
Ответ:
\(
BC = 3 \, \text{см}
\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.