ГДЗ по Геометрии 10 класс Номер 14 Атанасян — Подробные Ответы

Три прямые проходят через одну точку. Через каждые две из них проведена плоскость. Сколько всего проведено плоскостей?

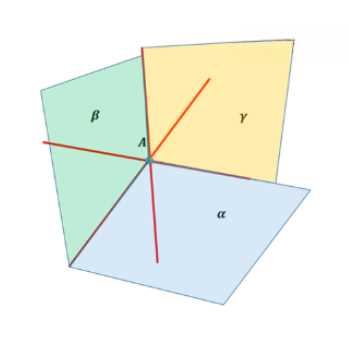
Через любые две из трёх прямых, проходящих через точку \(A\), можно провести плоскость. Всего таких пар три, поэтому возможно проведение трёх плоскостей: \(\alpha\), \(\beta\), \(\gamma\). Однако, если все три прямые \(a\), \(b\), \(c\) лежат в одной плоскости, то вместо трёх плоскостей будет одна.

Ответ: либо \(3\) плоскости, либо \(1\) плоскость.

Дано три прямые, проходящие через одну точку \(A\). Через каждые две прямые проведена плоскость. Нужно определить общее количество плоскостей.

Рассмотрим ситуацию:

Пусть прямые обозначены как \(a\), \(b\), \(c\), и они проходят через точку \(A\).

1. Через любые две прямые можно провести единственную плоскость, так как две пересекающиеся прямые определяют плоскость. Таким образом:
— Через прямые \(a\) и \(b\) проходит плоскость \(\alpha\),
— Через прямые \(a\) и \(c\) проходит плоскость \(\beta\),
— Через прямые \(b\) и \(c\) проходит плоскость \(\gamma\).

На данном этапе мы видим, что может быть проведено три плоскости.

2. Однако, существует исключение: если третья прямая лежит в плоскости, образованной первыми двумя прямыми, то все три прямые лежат в одной плоскости. В этом случае вместо трёх плоскостей будет одна общая плоскость.

Таким образом, возможны два случая:
1. Если прямые \(a\), \(b\), \(c\) не лежат в одной плоскости, то общее количество плоскостей равно трём: \(\alpha\), \(\beta\), \(\gamma\).
2. Если прямые \(a\), \(b\), \(c\) лежат в одной плоскости, то общее количество плоскостей равно одной.

Ответ: количество плоскостей — либо три, либо одна, в зависимости от взаимного расположения прямых.