ГДЗ по Геометрии 10 класс Номер 139 Атанасян — Подробные Ответы

Из некоторой точки проведены к плоскости две наклонные. Докажите, что:
а) если наклонные равны, то равны и их проекции;
б) если проекции наклонных равны, то равны и наклонные;
в) если наклонные не равны, то большая наклонная имеет большую проекцию.

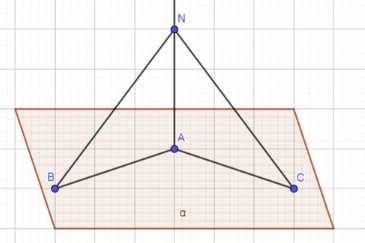
Дано: \(NB, NC\) — наклонные; \(NA \perp \alpha\).
Требуется доказать:
\(a)\) \(AC = AB\);
\(б)\) \(NC = NB\);
\(в)\) \(AB > AC\).

Доказательство:

\(a)\) Рассмотрим \(\triangle NAB\) и \(\triangle NCA\) — прямоугольные:
\(
NB = NC \quad \text{и} \quad NA \quad \text{общая}.
\)
Следовательно, \(\triangle NAB = \triangle NCA\) (по двум катетам).
Отсюда \(BA = AC\), что и требовалось доказать.

\(б)\) Рассмотрим \(\triangle NAB\) и \(\triangle NCA\) — прямоугольные:
\(
AB = AC \quad \text{и} \quad NA \quad \text{общая}.
\)
Следовательно, \(\triangle NAB = \triangle NCA\) (по двум катетам).
Отсюда \(NB = NC\), что и требовалось доказать.

\(в)\) Рассмотрим \(\triangle NAB\) и \(\triangle NCA\) — прямоугольные:
Если \(NB > NC\), то:
\(
AB = \sqrt{NB^2 — NA^2}, \quad AC = \sqrt{NC^2 — NA^2}.
\)
Так как \(NB^2 > NC^2\), то:
\(
NB^2 — NA^2 > NC^2 — NA^2.
\)
Следовательно:
\(
AB > AC,
\)
что и требовалось доказать.

Дано: \(NB\) и \(NC\) — наклонные, \(NA \perp \alpha\). Требуется доказать три утверждения: \(AC = AB\), \(NC = NB\) и \(AB > AC\). Рассмотрим каждое утверждение последовательно и подробно.

Рассмотрим первое утверждение \(AC = AB\). Треугольники \(\triangle NAB\) и \(\triangle NCA\) являются прямоугольными, так как \(NA \perp \alpha\). В этих треугольниках катеты \(NB\) и \(NC\) равны (\(NB = NC\)), а гипотенуза \(NA\) является общей стороной. Поскольку две стороны в треугольниках равны, то по признаку равенства треугольников по двум катетам \(\triangle NAB = \triangle NCA\). Это означает, что их соответствующие элементы равны, в частности \(AB = AC\). Таким образом, первое утверждение доказано.

Теперь рассмотрим второе утверждение \(NC = NB\). Треугольники \(\triangle NAB\) и \(\triangle NCA\) снова являются прямоугольными, так как \(NA \perp \alpha\). В этих треугольниках гипотенуза \(NA\) является общей, а катеты \(AB\) и \(AC\) равны (\(AB = AC\)), что было доказано в первом утверждении. По признаку равенства треугольников по двум катетам \(\triangle NAB = \triangle NCA\). Это означает, что их соответствующие элементы равны, в частности \(NB = NC\). Второе утверждение также доказано.

Рассмотрим третье утверждение \(AB > AC\). Предположим, что \(NB > NC\). Тогда длины сторон \(AB\) и \(AC\) можно выразить через теорему Пифагора:
\(AB = \sqrt{NB^2 — NA^2}\),
\(AC = \sqrt{NC^2 — NA^2}\).

Так как \(NB > NC\), то \(NB^2 > NC^2\). Если из обеих сторон этого неравенства вычесть одинаковое значение \(NA^2\), то получится:
\(NB^2 — NA^2 > NC^2 — NA^2\).

Из этого следует, что:
\(\sqrt{NB^2 — NA^2} > \sqrt{NC^2 — NA^2}\),
то есть \(AB > AC\). Таким образом, третье утверждение также доказано.

Все три утверждения доказаны.