
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 138 Атанасян — Подробные Ответы
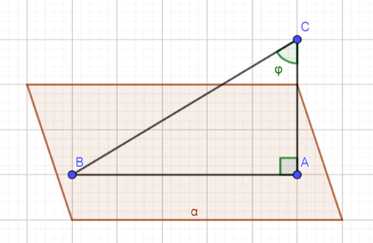
Из некоторой точки проведены к данной плоскости перпендикуляр и наклонная, угол между которыми равен \(\varphi\).
а) Найдите наклонную и её проекцию на данную плоскость, если перпендикуляр равен \(d\).
б) Найдите перпендикуляр и проекцию наклонной, если наклонная равна \(m\).
Дано:
\( AC \perp \alpha \), \( AB \) — наклонная,
\(\angle BAC = \varphi\), \( AC = d \) (в пункте а), \( AB = m \) (в пункте б).
Найти:
а) \( AB, BC \);
б) \( AC, BC \).
Решение:
а) Рассмотрим \(\triangle ABC\) — прямоугольный:
\(
AC = d, \quad AB = \frac{d}{\cos \varphi}, \quad BC = d \cdot \tan \varphi.
\)
Это следует из соотношений сторон в прямоугольном треугольнике:
\(
\cos \varphi = \frac{AC}{AB}, \quad \tan \varphi = \frac{BC}{AC}.
\)
Подставляя известные значения, получаем:
\(
AB = \frac{d}{\cos \varphi}, \quad BC = d \cdot \tan \varphi.
\)
б) Рассмотрим \(\triangle ABC\) — прямоугольный:
\(
AB = m, \quad AC = m \cdot \cos \varphi, \quad BC = m \cdot \sin \varphi.
\)
Это также следует из соотношений сторон в прямоугольном треугольнике:
\(
\cos \varphi = \frac{AC}{AB}, \quad \sin \varphi = \frac{BC}{AB}.
\)
Подставляя известные значения, получаем:
\(
AC = m \cdot \cos \varphi, \quad BC = m \cdot \sin \varphi.
\)
Ответ:
а) \( AB = \frac{d}{\cos \varphi}, \quad BC = d \cdot \tan \varphi \);
б) \( AC = m \cdot \cos \varphi, \quad BC = m \cdot \sin \varphi \).
Дано, что \( AC \) перпендикулярно плоскости \( \alpha \), а \( AB \) — наклонная, то есть гипотенуза прямоугольного треугольника \( \triangle ABC \). Угол между наклонной \( AB \) и перпендикуляром \( AC \) обозначен как \( \varphi \). Задача состоит в нахождении неизвестных сторон треугольника \( \triangle ABC \) с использованием тригонометрических соотношений.
Для решения задачи необходимо вспомнить основные тригонометрические функции для прямоугольного треугольника:
1. \( \cos \varphi = \frac{\text{прилежащий катет}}{\text{гипотенуза}} \), то есть \( \cos \varphi = \frac{AC}{AB} \).
2. \( \sin \varphi = \frac{\text{противолежащий катет}}{\text{гипотенуза}} \), то есть \( \sin \varphi = \frac{BC}{AB} \).
3. \( \tan \varphi = \frac{\text{противолежащий катет}}{\text{прилежащий катет}} \), то есть \( \tan \varphi = \frac{BC}{AC} \).
В пункте а дано, что \( AC = d \). Используя тригонометрические соотношения:
\( \cos \varphi = \frac{AC}{AB} \). Отсюда можно выразить \( AB \):
\( AB = \frac{AC}{\cos \varphi} \). Подставляя \( AC = d \), получаем:
\( AB = \frac{d}{\cos \varphi} \).
\( \tan \varphi = \frac{BC}{AC} \). Отсюда можно выразить \( BC \):
\( BC = AC \cdot \tan \varphi \). Подставляя \( AC = d \), получаем:
\( BC = d \cdot \tan \varphi \).
Таким образом, в пункте а:
\( AB = \frac{d}{\cos \varphi} \), \( BC = d \cdot \tan \varphi \).
В пункте б дано, что \( AB = m \). Используя тригонометрические соотношения:
\( \cos \varphi = \frac{AC}{AB} \). Отсюда можно выразить \( AC \):
\( AC = AB \cdot \cos \varphi \). Подставляя \( AB = m \), получаем:
\( AC = m \cdot \cos \varphi \).
\( \sin \varphi = \frac{BC}{AB} \). Отсюда можно выразить \( BC \):
\( BC = AB \cdot \sin \varphi \). Подставляя \( AB = m \), получаем:
\( BC = m \cdot \sin \varphi \).
Таким образом, в пункте б:
\( AC = m \cdot \cos \varphi \), \( BC = m \cdot \sin \varphi \).
Ответ полностью основан на применении тригонометрических функций и их определениях в прямоугольном треугольнике. Все вычисления выполняются путем подстановки известных значений и использования формул.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!