
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 137 Атанасян — Подробные Ответы
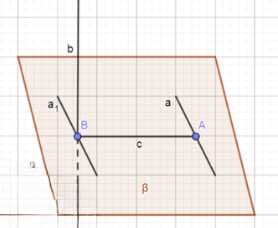
Докажите, что через каждую из двух взаимно перпендикулярных скрещивающихся прямых проходит плоскость, перпендикулярная к другой прямой.
Пусть \(a \perp b\) и \(a \not\parallel b\).
На прямой \(a\) отметим точку \(A\) и из нее опустим перпендикуляр \(c\) на прямую \(b\). Пусть \(c \cap b = B\), тогда \(AB \perp b\).
Через точку \(B\) проведем прямую \(a_1 \parallel a\). Так как \(a \perp b\), то \(a_1 \perp b\).
Через прямую \(a_1\) и точку \(A\) проведем плоскость \(\beta\). Докажем, что \(\beta \perp b\): \(A \in \beta\), \(B \in \beta\), следовательно, \(AB \in \beta\) и \(AB \perp b\); \(a_1 \in \beta\) и \(a_1 \perp b\), значит, \(b \perp \beta\).
Докажем, что \(a \in \beta\): \(a_1 \parallel a\), \(a_1 \in \beta\), значит, либо \(a \in \beta\), либо \(a \parallel \beta\). Так как \(a\) и \(b\) имеют общую точку \(A\), то \(a \not\parallel \beta\), следовательно, \(a \in \beta\).
Таким образом, через прямую \(a\) проходит единственная плоскость, перпендикулярная \(b\). Аналогично через \(b\) проводим плоскость, перпендикулярную \(a\).
Для решения задачи подробно разберем каждый шаг:
Пусть \(a \perp b\) и \(a \not\parallel b\).
На прямой \(a\) отметим точку \(A\) и из нее опустим перпендикуляр \(c\) на прямую \(b\). Согласно теореме, через заданную точку проходит единственная прямая, перпендикулярная данной. Пусть \(c \cap b = B\). Тогда \(AB \perp b\).
Через точку \(B\) проведем прямую \(a_1 \parallel a\). Согласно теореме о прямых в пространстве, через любую точку пространства, не лежащую на данной прямой, проходит единственная прямая, параллельная данной. Так как \(a \perp b\), то \(a_1 \perp b\) (по лемме о параллельных и перпендикулярных прямых).
Через прямую \(a_1\) и точку \(A\) проведем плоскость \(\beta\). Докажем, что плоскость \(\beta\) перпендикулярна \(b\).
Точки \(A \in \beta\) и \(B \in \beta\), следовательно, \(AB \in \beta\). Из условия \(AB \perp b\). Также \(a_1 \in \beta\) и \(a_1 \perp b\). Пересечение \(a_1 \cap AB = B\). Таким образом, \(b \perp \beta\) (по признаку перпендикулярности прямой и плоскости).
Докажем, что \(a \in \beta\).
Из условия \(a_1 \parallel a\) и \(a_1 \in \beta\), следовательно, либо \(a \in \beta\), либо \(a \parallel \beta\). Однако \(a\) и \(b\) имеют общую точку \(A\), поэтому они не могут быть параллельны. Остается единственный вариант: \(a \in \beta\).
Таким образом, через прямую \(a\) проходит единственная плоскость, перпендикулярная \(b\).
Аналогично, через прямую \(b\) можно провести единственную плоскость, перпендикулярную \(a\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!