
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 136 Атанасян — Подробные Ответы
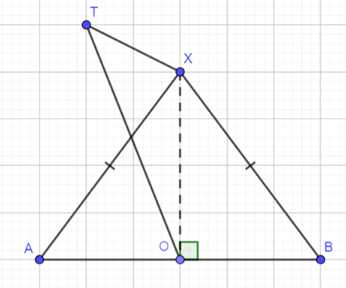
Докажите, что если точка Х равноудалена от концов данного отрезка АВ, то она лежит в плоскости, проходящей через середину отрезка АВ и перпендикулярной к прямой АВ.
Дано: \(X \in AB\), \(AO = OB = \frac{AB}{2}\), \(AX = BX\).
Доказать: \(X \in TOX\), \(TOX \perp AB\).
Рассмотрим \(\triangle AXB\):
\(AX = BX\), следовательно, \(\triangle AXB\) — равнобедренный.
Опустим высоту \(XO\), тогда \(XO\) — медиана, биссектриса и высота (по свойству равнобедренного треугольника), значит \(AO = OB\).
Построим перпендикуляр \(TO \perp \triangle AXB\):
Прямые \(OT\) и \(OX\) лежат в одной плоскости, так как пересекаются.
\(AO \perp OX\) и \(AO \perp OT\), следовательно, \(AB \perp TOX\).
Так как \(AB \perp TOX\), \(X \in TOX\) и \(O \in TOX\), то \(\triangle ABX\) и \(\triangle TOX\) пересекаются по прямой \(XO\), что и требовалось доказать.
Дано: \(X \in AB\), \(AO = OB = \frac{AB}{2}\), \(AX = BX\).
Доказать: \(X \in TOX\), \(TOX \perp AB\).
Рассмотрим треугольник \(AXB\). Так как \(AX = BX\), треугольник \(AXB\) является равнобедренным. В равнобедренном треугольнике высота, проведённая из вершины к основанию, одновременно является медианой, биссектрисой и высотой. Опустим высоту \(XO\) из вершины \(X\) на основание \(AB\). Тогда \(XO\) делит \(AB\) пополам и выполняет роль медианы. Следовательно, \(AO = OB\). Также \(XO\) является биссектрисой угла \(AXB\), так как делит угол пополам, и высотой, так как \(XO \perp AB\).
Построим перпендикуляр \(TO\), который будет перпендикулярен плоскости треугольника \(AXB\). Прямые \(OT\) и \(OX\) лежат в одной плоскости, так как они пересекаются в точке \(O\). Это позволяет рассматривать их взаимное расположение в пространстве.
Так как \(AO \perp OX\) и \(AO \perp OT\), то отрезок \(AB\), проходящий через точки \(A\) и \(B\), будет перпендикулярен плоскости \(TOX\). Таким образом, \(AB \perp TOX\).
Учитывая, что \(AB \perp TOX\), а точка \(X\) принадлежит прямой \(AB\), то точка \(X\) также принадлежит плоскости \(TOX\). Точка \(O\), как точка пересечения высоты \(XO\) и перпендикуляра \(TO\), также лежит в плоскости \(TOX\).
Плоскости треугольника \(ABX\) и \(TOX\) пересекаются по прямой \(XO\), которая является общей для обеих плоскостей. Это доказывает, что точка \(X\) принадлежит плоскости \(TOX\), а плоскость \(TOX\) перпендикулярна прямой \(AB\), что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!