
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 130 Атанасян — Подробные Ответы
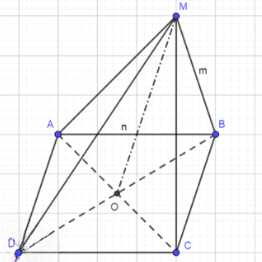
Через вершину В квадрата ABCD проведена прямая ВМ. Известно, что ∠MBA = ∠MBC = 90°, MB = m, AB = n. Найдите расстояния от точки М до:
а) вершин квадрата;
б) прямых AC и BD.
Дано: \(ABCD\) — квадрат, \(BM \perp AB\), \(\angle MBA = 90^\circ\), \(\angle MBC = 90^\circ\), \(MB = m\), \(AB = n\). Найти:
\(a)\) \(MA, MB, MC, MD\);
\(b)\) \(p(M, AC), p(M, BD)\).
Решение:
Рассмотрим \(\triangle ABCM\) и \(\triangle ABMA\) — прямоугольные:
\(
CM = AM = \sqrt{m^2 + n^2}.
\)
Рассмотрим \(\triangle DBM\) — прямоугольный:
\(
DM = \sqrt{BM^2 + DB^2}, \quad DB = \sqrt{n^2 + n^2} = n\sqrt{2}, \quad DM =\)
\(= \sqrt{2n^2 + m^2}.
\)
Расстояние от точки до прямой:
\(
p(M, BD) = MB = m.
\)
В \(\triangle BMO\) и прямой \(AC\):
\(
p(M, AC) = OM, \quad OM = \sqrt{BM^2 + BO^2}, \quad BO = \frac{n\sqrt{2}}{2},\)
\( \quad OM = \sqrt{m^2 + \frac{n^2}{2}}.
\)
Ответ:
\(a)\) \(AM = \sqrt{m^2 + n^2}, \, DM = \sqrt{2n^2 + m^2}\);
\(b)\) \(p(M, BD) = m, \, p(M, AC) = \sqrt{m^2 + \frac{n^2}{2}}\).
Дано: \(ABCD\) — квадрат, \(BM \perp AB\), \(\angle MBA = 90^\circ\), \(\angle MBC = 90^\circ\), \(MB = m\), \(AB = n\). Требуется найти длины \(MA, MB, MC, MD\), а также расстояния от точки \(M\) до диагоналей \(AC\) и \(BD\).
Рассмотрим треугольники \(\triangle ABCM\) и \(\triangle ABMA\). Они прямоугольные, так как \(ABCD\) — квадрат, а \(BM\) перпендикулярен сторонам \(AB\) и \(BC\). В этих треугольниках гипотенузы \(AM\) и \(CM\) равны, так как \(AB = BC = n\), а \(BM\) является общей стороной. Используем теорему Пифагора:
\(
AM = CM = \sqrt{BM^2 + AB^2} = \sqrt{m^2 + n^2}.
\)
Теперь рассмотрим треугольник \(\triangle DBM\), который также является прямоугольным. Здесь гипотенуза \(DM\) ищется через теорему Пифагора:
\(
DM = \sqrt{BM^2 + DB^2}.
\)
Диагональ квадрата \(DB\) равна:
\(
DB = \sqrt{AB^2 + BC^2} = \sqrt{n^2 + n^2} = n\sqrt{2}.
\)
Подставляем значение \(DB\) в формулу для \(DM\):
\(
DM = \sqrt{BM^2 + DB^2} = \sqrt{m^2 + (n\sqrt{2})^2} = \sqrt{m^2 + 2n^2}.
\)
Для нахождения расстояния от точки \(M\) до диагонали \(BD\) заметим, что \(BM\) перпендикулярен \(BD\), так как \(BM \perp AB\), а \(BD\) делит угол между \(AB\) и \(BC\) пополам. Следовательно, расстояние от \(M\) до \(BD\) равно длине \(BM\):
\(
p(M, BD) = MB = m.
\)
Теперь найдем расстояние от точки \(M\) до диагонали \(AC\). Диагональ \(AC\) делит квадрат на два равных прямоугольных треугольника, а также делит угол между сторонами \(AB\) и \(BC\) пополам. В таком случае расстояние от \(M\) до \(AC\) равно длине перпендикуляра из \(M\) на \(AC\). Обозначим основание этого перпендикуляра как \(O\). Точка \(O\) лежит на \(AC\), а треугольник \(\triangle BMO\) является прямоугольным.
Используем теорему Пифагора для нахождения \(OM\):
\(
OM = \sqrt{BM^2 + BO^2}.
\)
Диагональ \(AC\) равна \(n\sqrt{2}\), а точка \(O\) делит её пополам, так как \(O\) является серединой \(AC\). Тогда:
\(
BO = \frac{AC}{2} = \frac{n\sqrt{2}}{2}.
\)
Подставляем значение \(BO\) в формулу для \(OM\):
\(
OM = \sqrt{BM^2 + BO^2} = \sqrt{m^2 + \left(\frac{n\sqrt{2}}{2}\right)^2} = \sqrt{m^2 + \frac{n^2}{2}}.
\)
Таким образом, расстояние от точки \(M\) до диагонали \(AC\) равно \(OM\):
\(
p(M, AC) = \sqrt{m^2 + \frac{n^2}{2}}.
\)
Ответ:
\(AM = \sqrt{m^2 + n^2}\), \(DM = \sqrt{2n^2 + m^2}\), \(p(M, BD) = m\), \(p(M, AC) = \sqrt{m^2 + \frac{n^2}{2}}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!