ГДЗ по Геометрии 10 класс Номер 129 Атанасян — Подробные Ответы

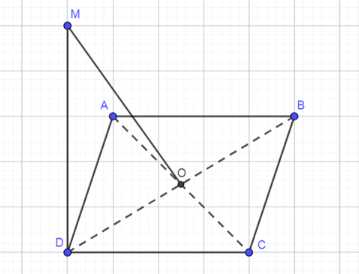
Прямая АМ перпендикулярна к плоскости квадрата ABCD, диагонали которого пересекаются в точке О. Докажите, что: а) прямая BD перпендикулярна к плоскости АМО; б) МО ⊥ BD.

Дано: \(ABCD\) — квадрат, следовательно:
\(
AC \perp BD \, (\text{по свойству диагоналей квадрата});
\)
\(
AC \perp BD \, \text{и} \, O \in AC, \, \text{следовательно} \, BD \perp AO;
\)
\(
MA \perp ABC \, \text{и} \, BD \in ABC, \, \text{значит} \, BD \perp MA.
\)

\(a)\) \(BD \perp MA\) и \(BD \perp AO\), \(AO\) и \(MA \in AMO\) и \(AO \cap MA = A\), следовательно:
\(
BD \perp AMO \, (\text{по признаку перпендикулярности прямой и плоскости}).
\)

\(б)\) \(MO \in AMO\) и \(BD \perp AMO\), следовательно:
\(
BD \perp MO, \, \text{что и требовалось доказать}.
\)

Дано, что \(ABCD\) — квадрат. Это означает, что все его стороны равны, углы прямые, а диагонали равны и пересекаются под прямым углом в точке \(O\). По свойству диагоналей квадрата, они всегда перпендикулярны. Следовательно, \(AC \perp BD\). Так как точка \(O\) является точкой пересечения диагоналей, то \(O \in AC\) и \(O \in BD\). Из этого следует, что прямая \(BD\) перпендикулярна прямой \(AO\).

По условию, \(AM \perp ABCD\). Это значит, что \(AM\) перпендикулярна любой прямой, лежащей в плоскости квадрата \(ABCD\), включая диагональ \(AC\). Кроме того, \(MA \perp ABC\), а \(BD \in ABC\). Так как \(BD\) принадлежит плоскости \(ABC\), а \(MA\) перпендикулярна этой плоскости, то \(BD \perp MA\).

Теперь докажем пункт (a). У нас уже есть, что \(BD \perp MA\) и \(BD \perp AO\). Прямые \(AO\) и \(MA\) лежат в плоскости \(AMO\), а их пересечение — это точка \(A\). Таким образом, \(BD\) перпендикулярна двум пересекающимся прямым, принадлежащим плоскости \(AMO\). По признаку перпендикулярности прямой и плоскости, если прямая перпендикулярна двум пересекающимся прямым в плоскости, то она перпендикулярна всей плоскости. Следовательно, \(BD \perp AMO\).

Теперь докажем пункт (б). Точка \(M\) лежит на прямой \(AM\), а точка \(O\) лежит на прямой \(AO\). Таким образом, отрезок \(MO\) полностью принадлежит плоскости \(AMO\). Из пункта (a) мы уже доказали, что \(BD \perp AMO\). Это означает, что \(BD\) перпендикулярна любой прямой, лежащей в плоскости \(AMO\), включая прямую \(MO\). Следовательно, \(BD \perp MO\).

Таким образом, оба пункта доказаны.