Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 127 Атанасян — Подробные Ответы
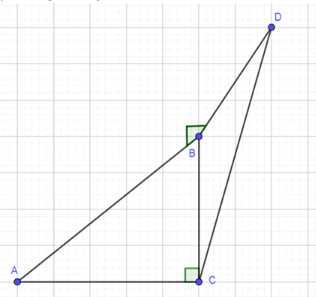
В треугольнике АВС сумма углов А и В равна 90°. Прямая BD перпендикулярна к плоскости АВС. Докажите, что CD ⊥ AC.
Дано: \(\triangle ABC\), \(\angle A + \angle B = 90^\circ\), \(BD \perp \triangle ABC\).
Доказать: \(CD \perp AC\).
Рассмотрим \(\triangle ABC\):
\(\angle C = 180^\circ — (\angle A + \angle B) = 180^\circ — 90^\circ = 90^\circ\) (по теореме о сумме углов в треугольнике), отсюда \(AC \perp BC\).
\(BD \perp \triangle ABC\) и \(AC \in \triangle ABC\), следовательно, \(BD \perp AC\).
\(AC \perp BC\) и \(AC \perp BD\), следовательно, \(AC \perp \triangle BCD\).
\(AC \perp \triangle BCD\) и \(CD \in \triangle BCD\), следовательно, \(CD \perp AC\), что и требовалось доказать.
Дано:
\(\triangle ABC\), \(\angle A + \angle B = 90^\circ\), \(BD \perp \triangle ABC\).
Доказать: \(CD \perp AC\).
Рассмотрим треугольник \(\triangle ABC\). По теореме о сумме углов треугольника сумма всех углов равна \(180^\circ\). Учитывая, что \(\angle A + \angle B = 90^\circ\), можно найти угол \(\angle C\):
\(\angle C = 180^\circ — (\angle A + \angle B) = 180^\circ — 90^\circ = 90^\circ\).
Таким образом, треугольник \(\triangle ABC\) является прямоугольным, а сторона \(AC\) перпендикулярна стороне \(BC\), то есть \(AC \perp BC\).
Из условия известно, что \(BD \perp \triangle ABC\). Это означает, что прямая \(BD\) перпендикулярна любой прямой, лежащей в плоскости треугольника \(\triangle ABC\), включая сторону \(AC\). Следовательно, \(BD \perp AC\).
Поскольку \(AC \perp BC\) и \(AC \perp BD\), то сторона \(AC\
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.