
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 126 Атанасян — Подробные Ответы
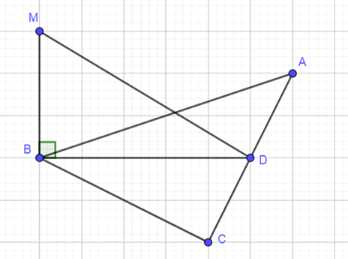
Прямая МВ перпендикулярна к сторонам АВ и ВС треугольника АВС. Определите вид треугольника MBD, где D — произвольная точка прямой АС.
Дано: ΔABC; MB 1 AB; MB 1 BC; DE AC;
Определить: вид AMBD -?;
Решение:
1) MB 1 AB и MB 1 CB, CB и AB Є АВС и СВ n АВ = В, следовательно МВ 1 ABC (по признаку перпендикулярности прямой и плоскости); 2) МВ 1 ABC и BD E ABC, следовательно MB I BD, значит \(\angle MBD = 90°\), следовательно AMBD — прямоугольный;
Ответ: AMBD — прямоугольный.
Дано: ΔABC; MB 1 AB; MB 1 BC; DE AC;
Определить: вид AMBD -?;
Решение:
Рассмотрим треугольник ABC. Известно, что прямая MB перпендикулярна сторонам AB и BC треугольника ABC, то есть MB 1 AB и MB 1 BC. Это означает, что прямая MB перпендикулярна плоскости треугольника ABC, то есть MB 1 ABC (по признаку перпендикулярности прямой и плоскости).
Далее, поскольку прямая MB перпендикулярна плоскости треугольника ABC, и точка D лежит на этой плоскости, то прямая MB также перпендикулярна прямой BD, то есть MB 1 BD (по признаку перпендикулярности прямой и плоскости). Следовательно, угол MBD является прямым углом, то есть \(\angle MBD = 90°\).
Таким образом, треугольник AMBD является прямоугольным треугольником, поскольку один из его углов (угол MBD) равен 90°.
Ответ: AMBD — прямоугольный.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!