Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 125 Атанасян — Подробные Ответы
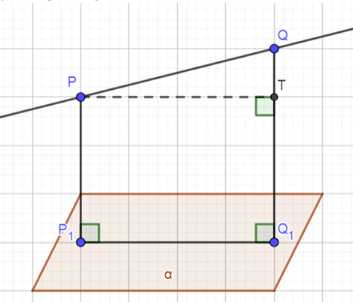
Через точки Р и Q прямой PQ проведены прямые, перпендикулярные к плоскости о и пересекающие её соответственно в точках Р1 и Q1. Найдите PiQ1, если PQ = 15 см, РР1 = 21,5 см, QQ1 = 33,5 см
Дано: PP1 ⊥ a и QQ1 ⊥ a, следовательно PP1 ∥ Q1 (как перпендикуляры к одной плоскости), тогда PP1 и Q1 принадлежат к одной плоскости P1Q1PQ; ∠P1Q1Q = P1Q1. Рассмотрим P1Q1PQ: PP1 ⊥ Q1, следовательно P1Q1QP — трапеция. Проведем высоту T. Рассмотрим PTP1Q1: ∠P1 = ∠T = 90°, значит ∠P = 90° (по теореме о сумме углов), следовательно PTP1Q1 — прямоугольник, отсюда PT = P1Q1; TQ1 = PP1 = 21,5 см. Рассмотрим ∆TPQ — прямоугольный: QT = Q1 — TQ1 = 33,5 — 21,5 = 12 см; PT = P1Q1 = \(\sqrt{15^2 — 12^2} = \sqrt{81} = 9\) см. Ответ: P1Q1 = 9 см.
Дано: PP1 ⊥ a и QQ1 ⊥ a, следовательно PP1 ∥ Q1 (как перпендикуляры к одной плоскости), тогда PP1 и Q1 принадлежат к одной плоскости P1Q1PQ; ∠P1Q1Q = P1Q1.
Рассмотрим P1Q1PQ: PP1 ⊥ Q1, следовательно P1Q1QP — трапеция. Проведем высоту T.
Рассмотрим PTP1Q1: ∠P1 = ∠T = 90°, значит ∠P = 90° (по теореме о сумме углов), следовательно PTP1Q1 — прямоугольник, отсюда PT = P1Q1; TQ1 = PP1 = 21,5 см.
Рассмотрим ∆TPQ — прямоугольный:
QT = Q1 — TQ1 = 33,5 — 21,5 = 12 см;
PT = P1Q1 = \(\sqrt{15^2 — 12^2} = \sqrt{81} = 9\) см.
Ответ: P1Q1 = 9 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.