
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 121 Атанасян — Подробные Ответы
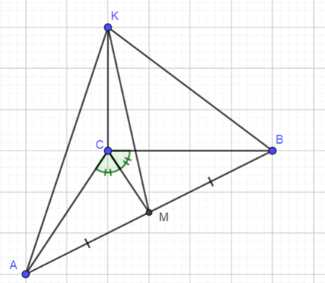
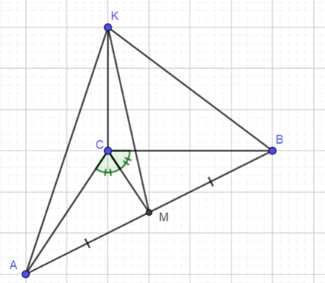
В треугольнике АВС дано: \(\angle C = 90^\circ\), АС = 6 см, ВС = 8 см, СМ — медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС, причём СК = 12 см. Найдите КМ.
Дано: ΔABC; ∠C = 90°; AC = 6 см; BC = 8 см; CM — медиана; CK ⊥ ABC; CK = 12 см; Найти: KM -?;
Решение:
1) CM — медиана, следовательно AM = MB, отсюда AM = \(\frac{1}{2}\) AB;
2) Рассмотрим ΔABC: AB^2 = 64 + 36 = 100 => AB = 10 см; AM = \(\frac{1}{2}\) · 10 = 5 см; \(\cos \angle A = \frac{AC}{AB} = \frac{6}{10} = \frac{3}{5}\);
3) По теореме косинусов: CM^2 = AM^2 + AC^2 — 2 · \(\cos \angle A\) · AM · AC; CM = \(\sqrt{6^2 + 5^2 — 2 \cdot \frac{3}{5} \cdot 6 \cdot 5}\) = \(\sqrt{36 + 25 — 36}\) = \(\sqrt{25}\) = 5 см;
4) Рассмотрим ΔKMC: KM = \(\sqrt{CM^2 + KC^2}\) = \(\sqrt{5^2 + 12^2}\) = \(\sqrt{25 + 144}\) = \(\sqrt{169}\) = 13 см;
Ответ: KM = 13 см.
Дано, что треугольник ABC является прямоугольным, где угол C равен 90 градусам. Длины сторон AC и BC равны 6 см и 8 см соответственно. Также известно, что CM является медианой треугольника, и CK перпендикулярна к стороне AB треугольника ABC, а длина CK равна 12 см. Требуется найти длину отрезка KM.
Для решения этой задачи мы будем использовать свойства прямоугольных треугольников и теорему косинусов.
Во-первых, поскольку CM является медианой треугольника ABC, то AM = MB. Следовательно, AM = (1/2)AB.
Во-вторых, рассмотрим треугольник ABC. Используя теорему Пифагора, мы можем найти длину стороны AB: \(AB^2 = AC^2 + BC^2 = 6^2 + 8^2 = 36 + 64 = 100\), откуда AB = 10 см. Тогда AM = (1/2)AB = (1/2)10 = 5 см. Кроме того, мы можем найти косинус угла A: \(\cos(A) = AC/AB = 6/10 = 3/5\).
В-третьих, применим теорему косинусов к треугольнику ACM, чтобы найти длину CM:
\(CM^2 = AM^2 + AC^2 — 2\cos(A)AM\cdot AC = 5^2 + 6^2 — 2\cdot(3/5)\cdot 5\cdot 6 = \)
\(=25 + 36 — 36 = 25\), откуда CM = √25 = 5 см.
Наконец, рассмотрим треугольник KMC. Используя теорему Пифагора, мы можем найти длину KM: \(KM^2 = CM^2 + KC^2 = 5^2 + 12^2 = 25 + 144 = 169\), откуда KM = √169 = 13 см.
Таким образом, длина отрезка KM равна 13 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!