
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 120 Атанасян — Подробные Ответы
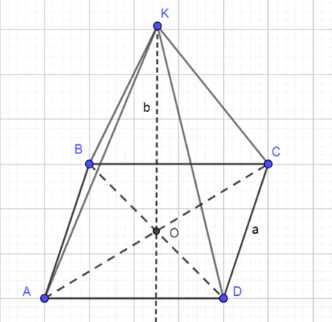
Через точку О пересечения диагоналей квадрата, сторона которого равна а, проведена прямая ОК, перпендикулярная к плоскости квадрата. Найдите расстояние от точки К до вершин квадрата, если ОК = b.
Дано: квадрат ABCD со стороной AB = a, точка O — пересечение диагоналей, перпендикуляр KO ⊥ ABCD, длина KO = b. Требуется найти длины отрезков KB, KA, KD, KC.
Так как ABCD — квадрат, его диагонали AC и BD пересекаются под прямым углом и делятся пополам в точке O. Следовательно, длины сторон OB, OD, OC и OA равны: \(OB = OD = OC = OA = \frac{a\sqrt{2}}{2}\).
Рассмотрим прямоугольные треугольники ΔOAK, ΔOBK, ΔOSK и ΔODK. Они имеют общую сторону KO = b и равные катеты OB = OD = OC = OA. Поэтому по признаку равенства прямоугольных треугольников по двум сторонам и углу между ними, эти четыре треугольника равны. Отсюда следует, что \(KB = KA = KD = KC\).
Найдем длину стороны KB, применив теорему Пифагора к ΔOBK:
\(KB^2 = OK^2 + OB^2 = b^2 + \left(\frac{a\sqrt{2}}{2}\right)^2 = b^2 + \frac{a^2}{2}\)
\(KB = \sqrt{b^2 + \frac{a^2}{2}}\)
Таким образом, все искомые отрезки KB, KA, KD, KC имеют одинаковую длину:
\(\sqrt{b^2 + \frac{a^2}{2}}\)
Дано: квадрат ABCD со стороной AB = a, точка O — пересечение диагоналей, перпендикуляр KO ⊥ ABCD, длина KO = b. Требуется найти длины отрезков KB, KA, KD, KC.
Рассмотрим свойства квадрата ABCD. Так как ABCD — квадрат, его диагонали AC и BD пересекаются под прямым углом в точке O и делятся этой точкой пополам. Следовательно, длины сторон OB, OD, OC и OA равны: \(OB = OD = OC = OA = \frac{a\sqrt{2}}{2}\).
Теперь обратимся к прямоугольным треугольникам ΔOAK, ΔOBK, ΔOSK и ΔODK. Угол ∠O в каждом из этих треугольников равен 90°, так как KO перпендикулярна плоскости ABCD. Сторона KO = b является общей для всех четырех треугольников. Кроме того, так как ABCD — квадрат, то по свойству диагоналей квадрата имеем: OB = OD = OC = OA.
Применим признак равенства прямоугольных треугольников. Треугольники ΔOAK, ΔOBK, ΔOSK и ΔODK имеют равные стороны KO = b и равные катеты OB = OD = OC = OA. Согласно признаку равенства прямоугольных треугольников по двум сторонам и углу между ними, эти четыре треугольника равны. Следовательно, \(KB = KA = KD = KC\).
Теперь найдем длину стороны KB, применив теорему Пифагора к ΔOBK:
\(KB^2 = OK^2 + OB^2 = b^2 + \left(\frac{a\sqrt{2}}{2}\right)^2 = b^2 + \frac{a^2}{2}\)
\(KB = \sqrt{b^2 + \frac{a^2}{2}}\)
Таким образом, все искомые отрезки KB, KA, KD, KC имеют одинаковую длину:
\(\sqrt{b^2 + \frac{a^2}{2}}\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!