
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 119 Атанасян — Подробные Ответы
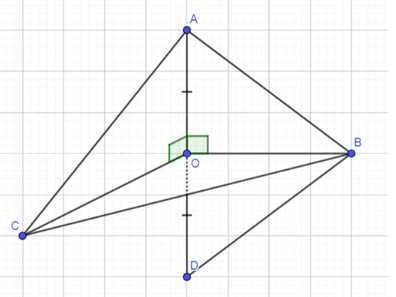
Прямая ОА перпендикулярна к плоскости ОВС, и точка О является серединой отрезка AD. Докажите, что:
a) AB = DB;
б) AB = AC, если ОВ = ОС;
в) ОВ = ОС, если АВ = AC.
Дано: 0A 1 OBC; AO = OD; б) ОВ = ОС; в) AB = AC;
Доказать: а) AB = DB; б) AB = AC; в) ОВ = ОС;
Доказательство: а) Рассмотрим AABD: AD I OB (так как OВ E BOC и AD I OВС), значит ОВ — высота AABD: АО = OD, следовательно, ОВ — медиана AABD, значит AABD — равнобедренный, отсюда АВ = BD;
б) Рассмотрим ДАОВ и ДАОС: АО I BOC и ВО, ОС є ВОС, следовательно АО I BO w AO 1 OC, значит \(\angle AOC = \angle AOB = 90°\); АО — общая сторона, ОВ = ОС (по условию), значит ДАОВ = ДАОС (по двум катетам), отсюда АС = СВ;
в) Рассмотрим ДАОВ и ДАОС: АО I BOС и BO, OC Є ВОС, следовательно АО I BO w AO I OC, значит \(\angle AOC = \angle AOB = 90°\); АО — общая сторона, АС = СВ (по условию), значит ДАОВ = ДАОС (по гипотенузе и катету), отсюда ОВ = ОС, что и требовалось доказать.
Дано: 0A 1 OBC; AO = OD; б) ОВ = ОС; в) AB = AC;
Доказать: а) AB = DB; б) AB = AC; в) ОВ = ОС;
Доказательство:
а) Рассмотрим треугольник AABD. Из условия известно, что AD I OB (так как OВ E BOC и AD I OВС), значит ОВ — высота треугольника AABD. Также известно, что АО = OD, следовательно, ОВ — медиана треугольника AABD. Так как медиана делит противоположную сторону пополам в равнобедренном треугольнике, то AABD — равнобедренный треугольник, и, следовательно, АВ = BD.
б) Рассмотрим треугольники ДАОВ и ДАОС. Из условия известно, что АО I BOC и ВО, ОС є ВОС, следовательно АО I BO и АО I OC. Это означает, что \(\angle AOC = \angle AOB = 90°\). Также известно, что АО — общая сторона, и ОВ = ОС (по условию). Следовательно, по двум равным катетам треугольники ДАОВ и ДАОС равны, и, значит, АС = СВ.
в) Рассмотрим треугольники ДАОВ и ДАОС. Из условия известно, что АО I BOС и BO, OC Є ВОС, следовательно АО I BO и АО I OC. Это означает, что \(\angle AOC = \angle AOB = 90°\). Также известно, что АО — общая сторона, и АС = СВ (по условию). Следовательно, по гипотенузе и катету треугольники ДАОВ и ДАОС равны, и, значит, ОВ = ОС, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!