ГДЗ по Геометрии 10 класс Номер 118 Атанасян — Подробные Ответы

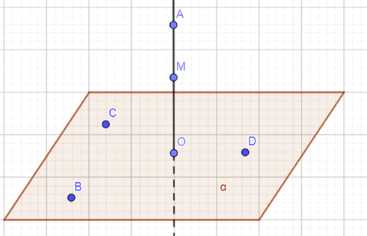
Точки А, М и О лежат на прямой, перпендикулярной к плоскости а, а точки O, B, C и D лежат в плоскости о. Какие из следующих углов являются прямыми: \(\angle AOB\), \(\angle MOC\), \(\angle DAM\), \(\angle DOA\), \(\angle BMO\)?

Дано: A, M, O ∈ AO; AO ⊥ a; O, B, C, D ∈ a.
Найти: прямые углы.

Решение:
1) Так как AO перпендикулярна a, то AO перпендикулярна любой прямой, лежащей внутри a.
2) O ∈ a, B ∈ a, C ∈ a, D ∈ a, следовательно прямые OB, OC и OD принадлежат a.
3) A ∈ AO; OB, OC, OD ∈ a, следовательно: \(\angle BOA = \angle AOC = \angle AOD = 90^\circ\).
4) A ∈ AO, D ∈ a, значит AD не принадлежит a, тогда \(\angle DAM \neq 90^\circ\).
5) M ∈ AO, B ∈ a, значит BM не принадлежит a, тогда \(\angle BMO \neq 90^\circ\).

Ответ: \(\angle BOA, \angle AOC, \angle AOD\).

Дано: точки A, M, O лежат на прямой AO, прямая AO перпендикулярна прямой a, точки O, B, C, D лежат на прямой a. Требуется найти прямые углы.

Решение:
Так как прямая AO перпендикулярна прямой a, то AO является перпендикуляром к прямой a. Это означает, что AO образует прямые углы со всеми прямыми, лежащими внутри угла, образованного прямой a. Поскольку точки O, B, C, D лежат на прямой a, прямые OB, OC и OD также принадлежат прямой a. Следовательно, углы \(\angle BOA\), \(\angle AOC\) и \(\angle AOD\) являются прямыми, то есть равными \(90^\circ\).

Далее, так как точка A лежит на прямой AO, а точка D лежит на прямой a, прямая AD не принадлежит прямой a. Поэтому угол \(\angle DAM\) не является прямым. Аналогично, поскольку точка M лежит на прямой AO, а точка B лежит на прямой a, прямая BM не принадлежит прямой a, и, следовательно, угол \(\angle BMO\) не является прямым.

Таким образом, прямыми углами в данной задаче являются \(\angle BOA\), \(\angle AOC\) и \(\angle AOD\).