
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 114 Атанасян — Подробные Ответы
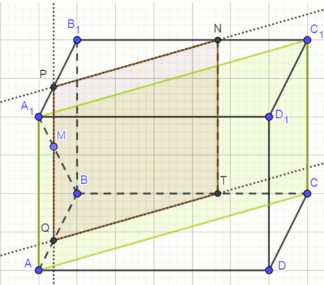
Изобразите параллелепипед ABCDA1B1C1D1 и отметьте на ребре АВ точку М. Постройте сечение параллелепипеда плоскостью, проходящей через точку М параллельно плоскости ACC1.
Сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точку M параллельно плоскости ACC1, представляет собой четырехугольник PNQT, где точки P, N, Q, T получены путем проведения прямых, параллельных ребрам параллелепипеда, через точку M.
Изобразим параллелепипед ABCDA1B1C1D1 и отметим на ребре AB точку M. Для построения сечения параллелепипеда плоскостью, проходящей через точку M параллельно плоскости ACC1, выполним следующие действия:
1) Проведем прямую PQ через точку M параллельно ребру A1A, пересекающую ребра A1B1 и AB в точках P и Q соответственно.
2) Проведем прямую PN параллельно ребру A1C1, пересекающую ребро B1C1 в точке N.
3) Проведем прямую QT параллельно ребру AC, пересекающую ребро BC в точке T.
4) Соединим точки P, N, Q, T, получив искомое сечение параллелепипеда плоскостью, проходящей через точку M параллельно плоскости ACC1.
Таким образом, сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точку M параллельно плоскости ACC1, представляет собой четырехугольник PNQT.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!