
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 112 Атанасян — Подробные Ответы
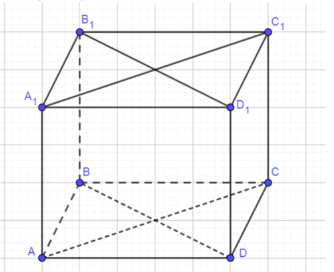
Докажите, что сумма квадратов четырёх диагоналей параллелепипеда равна сумме квадратов двенадцати его рёбер.
Дано: параллелепипед ABCDA1B1C1D1. Доказать: \(A1C^2 + B1D^2 + C1A^2 + BD^2 = 4AB^2 + 4AD^2 + 4A1A^2\).
Доказательство: Рассмотрим параллелограмм ABCD, для которого \(\angle ADC = 180° — \angle DAB\). Применяя теорему косинусов к треугольникам ABD и ACD, получим \(DB^2 = AD^2 + DC^2 — 2AD \cdot DC \cdot \cos \angle DAB\) и \(AC^2 = AD^2 + DC^2 — 2AD \cdot DC \cdot \cos \angle DAB\). Для прямоугольных треугольников DD1B1B и AA1CC1 справедливы теоремы Пифагора: \(D1B^2 + B1D^2 = 2DB^2 + 2B1B^2\) и \(A1C^2 + C1A^2 = 2AC^2 + 2A1A^2\). Сложив все равенства, получаем \(2DB^2 + 2B1B^2 + 2AC^2 + 2A1A^2 = 4DA^2 + 4A1A^2 + 4AB^2\), что и требовалось доказать.
Дано: параллелепипед ABCDA1B1C1D1. Доказать: \(A1C^2 + B1D^2 + C1A^2 + BD^2 = 4AB^2 + 4AD^2 + 4A1A^2\).
Доказательство: Рассмотрим параллелограмм ABCD. Согласно свойствам параллелограмма, противоположные стороны равны и параллельны, а диагонали пересекаются в точке, делящей их пополам. Следовательно, \(\angle ADC = 180° — \angle DAB\).
Рассмотрим треугольник ABD. Применяя теорему косинусов, получим: \(DB^2 = AD^2 + DC^2 — 2AD \cdot DC \cdot \cos \angle DAB\).
Аналогично, для треугольника ACD: \(AC^2 = AD^2 + DC^2 — 2AD \cdot DC \cdot \cos (180° — \angle DAB) = AD^2 + DC^2 -\)
\(-2AD \cdot DC \cdot \cos \angle DAB\).
Рассмотрим прямоугольный треугольник DD1B1B. Согласно теореме Пифагора: \(D1B^2 + B1D^2 = 2DB^2 + 2B1B^2\).
Рассмотрим прямоугольный треугольник AA1CC1. Согласно теореме Пифагора: \(A1C^2 + C1A^2 = 2AC^2 + 2A1A^2\).
Сложив все равенства, получим: \(2DB^2 + 2B1B^2 + 2AC^2 + 2A1A^2 = 2(DB^2 + AC^2) + 2A1A^2 + 2A1A^2 = \)
\(=4DA^2 + 4A1A^2 + 4AB^2\).
Таким образом, сумма квадратов четырех диагоналей параллелепипеда равна сумме квадратов двенадцати его ребер, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!