
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 111 Атанасян — Подробные Ответы
Докажите, что диагональ параллелепипеда меньше суммы трёх ребер, имеющих общую вершину.
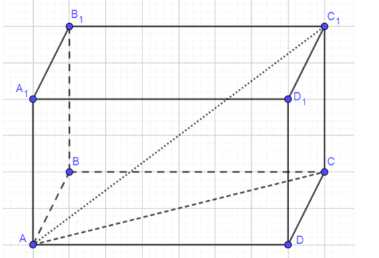
Пусть ABCDA₁B₁C₁D₁ — параллелепипед, где CA — диагональ, и AB, AA₁, AC — три ребра, имеющие общую вершину A. Докажем, что CA < AB + AA₁ + AC. Рассмотрим треугольник ABC, по неравенству треугольника AC < AB + BC, где BC = AD. Следовательно, AC < AB + AD. Рассмотрим треугольник ACC₁, по неравенству треугольника AC₁ < AC + C₁C, где C₁C = A₁A. Следовательно, AC₁ < A₁A + AC. Объединяя эти неравенства, получаем: CA < AB + AD и AC₁ < A₁A + AC. Складывая эти два неравенства, получаем: C₁A < AB + AA₁ + AC, что и требовалось доказать.
Для доказательства того, что диагональ параллелепипеда меньше суммы трёх рёбер, имеющих общую вершину, рассмотрим следующие шаги:
1) Пусть ABCDA₁B₁C₁D₁ — параллелепипед, где CA — диагональ, и AB, AA₁, AC — три ребра, имеющие общую вершину A.
2) Докажем, что CA < AB + AA₁ + AC. 3) Рассмотрим треугольник ABC. Согласно неравенству треугольника, AC < AB + BC, где BC = AD (так как ABCDA₁B₁C₁D₁ - параллелепипед). Следовательно, AC < AB + AD. 4) Рассмотрим треугольник ACC₁. Согласно неравенству треугольника, AC₁ < AC + C₁C, где C₁C = A₁A (так как ABCDA₁B₁C₁D₁ - параллелепипед). Следовательно, AC₁ < A₁A + AC. 5) Объединяя неравенства из пунктов 3 и 4, получаем: CA < AB + AD и AC₁ < A₁A + AC. 6) Складывая эти два неравенства, получаем: C₁A < AB + AA₁ + AC, что и требовалось доказать. Таким образом, мы показали, что диагональ параллелепипеда CA меньше суммы трёх рёбер AB, AA₁ и AC, имеющих общую вершину A.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!