Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 108 Атанасян — Подробные Ответы
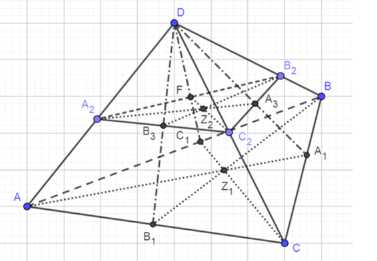
В тетраэдре DABC биссектрисы трёх углов при вершине D пересекают отрезки ВС, СА и АВ соответственно в точках А1, В1 и С1. Докажите, что отрезки AA1, BB1 и СС1 пересекаются в одной точке.
Дано, что в тетраэдре DABC биссектрисы трёх углов при вершине D пересекают стороны BC, CA и AB в точках A1, B1 и C1 соответственно. Требуется доказать, что отрезки AA1, BB1 и CC1 пересекаются в одной точке.
Для этого построим на сторонах BD, CD и AD точки A2, B2 и C2 так, чтобы DA2 = DB2 = DC2. Тогда треугольники AA2D, BB2D и CC2D будут равнобедренными, и их биссектрисы и медианы пересекутся в одной точке Z2. Аналогично, плоскости A2DZ2, B2DZ2 и C2DZ2 пересекаются по одной прямой DZ2. Наконец, можно показать, что отрезки AA1, BB1 и CC1 также пересекаются в одной точке Z1, лежащей на прямой DZ2, поскольку DAA1 ∩ DCC1 ∩ DBB1 = DZ2. Таким образом, доказано, что отрезки AA1, BB1 и CC1 пересекаются в одной точке.
Итак, для доказательства того, что отрезки AA1, BB1 и CC1 пересекаются в одной точке, мы можем использовать следующую логику:
1) Построим на сторонах BD, CD и AD точки A2, B2 и C2 соответственно так, чтобы DA2 = DB2 = DC2. Это значит, что треугольники AA2D и BB2D, BB2D и CC2D, CC2D и AA2D являются равнобедренными.
2) Отметим точки пересечения биссектрис этих равнобедренных треугольников: DC1 ∩ A2B2 = F, DA1 ∩ B2C2 = A3, DB1 ∩ A2C2 = B3.
3) Рассмотрим треугольник AA2B2D. Так как A2D = B2D, то этот треугольник является равнобедренным. Следовательно, DF является биссектрисой и медианой этого треугольника.
4) Аналогично, треугольники BB2C2D и CC2A2D также являются равнобедренными, и их биссектрисы и медианы пересекаются в одной точке Z2.
5) Таким образом, плоскости A2DZ2, B2DZ2 и C2DZ2 пересекаются по одной прямой DZ2.
6) Наконец, можно показать, что отрезки AA1, BB1 и CC1 также пересекаются в одной точке Z1, лежащей на прямой DZ2. Это следует из того, что DAA1 ∩ DCC1 ∩ DBB1 = DZ2.
Таким образом, мы доказали, что отрезки AA1, BB1 и CC1 пересекаются в одной точке Z1.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.