
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 107 Атанасян — Подробные Ответы
Изобразите тетраэдр ABCD и отметьте точку М на ребре АВ. Постройте сечение тетраэдра плоскостью, проходящей через точку М параллельно грани BDC.
Для построения сечения тетраэдра DABC плоскостью, проходящей через точку M на ребре AB параллельно грани BDC, выполним следующие действия:
Сначала мы изобразим тетраэдр DABC на чертеже. Это будет основное трехмерное геометрическое тело, с которым мы будем работать. Затем мы отметим точку M на ребре AB этого тетраэдра. Эта точка будет определять, через какую часть тетраэдра будет проходить секущая плоскость.
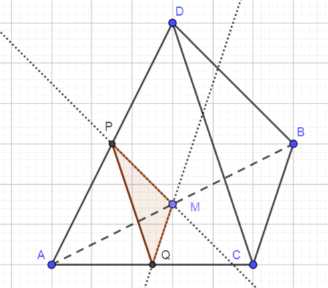
Следующим шагом мы проведем прямую MP, параллельную грани DB тетраэдра. Точка P будет лежать на пересечении этой прямой и грани AD тетраэдра. Проведение этой параллельной прямой позволит нам определить одну из сторон будущего сечения.
Далее мы проведем прямую MQ, параллельную грани BC тетраэдра. Точка Q будет лежать на пересечении этой прямой и грани AC тетраэдра. Проведение этой второй параллельной прямой позволит нам определить еще одну сторону будущего сечения.
Наконец, мы соединим точки P, Q и M. Полученный треугольник PQM и будет являться сечением тетраэдра DABC плоскостью, проходящей через точку M параллельно грани BDC.
Таким образом, мы последовательно построили сечение тетраэдра, используя параллельные прямые и точки их пересечения с гранями тетраэдра. Этот подход позволяет нам точно определить форму и положение секущей плоскости относительно исходного тетраэдра.
Для построения сечения тетраэдра DABC плоскостью, проходящей через точку M на ребре AB параллельно грани BDC, выполним следующие действия:
Сначала изобразим тетраэдр DABC и отметим точку M на ребре AB. Затем проведем прямую MP, параллельную грани DB. Точка P будет лежать на пересечении этой прямой и грани AD. Далее проведем прямую MQ, параллельную грани BC. Точка Q будет лежать на пересечении этой прямой и грани AC. Наконец, соединим точки P, Q и M, получив треугольник PQM, который и является сечением тетраэдра плоскостью, проходящей через точку M параллельно грани BDC.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!