
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 103 Атанасян — Подробные Ответы
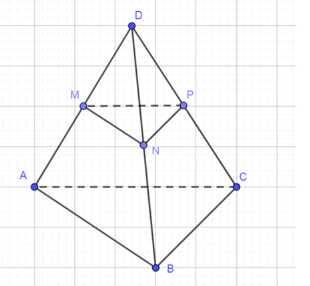
На рёбрах DA, DB и DC тетраэдра DABC отмечены точки М, N и Р так, что DM : MA = DN : NB = DP : PC. Докажите, что плоскости MNP и АВС параллельны. Найдите площадь треугольника MNP, если площадь треугольника АВС равна 10 см2 и DM : MA = =2:1.
Из подобия треугольников ADMP и ADAC, а также ADCB и ADPN следует, что плоскости треугольников МР и АС, а также PN и ВС параллельны. Это значит, что отношение сторон соответствующих треугольников равно:
\(\frac{MP}{AC} = \frac{PN}{BC} = \frac{MN}{AB} = \frac{\Delta MNP}{\Delta ABC}\)
\(\text{Коэффициент подобия равен }\frac{\Delta MNP}{\Delta ABC} = \frac{2}{3}\)
Для вычисления площади треугольника MNP будем использовать формулу площади через две стороны и угол между ними:
\(S_{MNP} = \frac{1}{2} \cdot MN \cdot NP \cdot \sin \angle MNP\)
\(\text{Где:}\)
\(MN = \frac{AB}{3}\)
\(NP = \frac{BC}{3}\)
\(\angle MNP = \angle ABC\)
\(\text{Подставляя значения, получаем:}\)
\(S_{MNP} = \frac{1}{2} \cdot \frac{AB}{3} \cdot \frac{BC}{3} \cdot \sin \angle ABC\)
\(S_{MNP} = \frac{ABC}{9} \cdot \sin \angle ABC\)
\(S_{MNP} = \frac{40}{9} \text{ см}^2\)
\(\text{Таким образом, окончательный ответ можно записать в виде смешанной дроби:}\)
\(4\frac{4}{9} \text{ см}^2\)
Из условия задачи известно, что треугольники ADMP и ADAC, а также ADCB и ADPN являются подобными. Это означает, что плоскости треугольников МР и АС, а также PN и ВС параллельны. Следовательно, отношение сторон соответствующих треугольников равно:
\(\frac{MP}{AC} = \frac{PN}{BC} = \frac{MN}{AB} = \frac{\Delta MNP}{\Delta ABC}\)
Коэффициент подобия, то есть отношение площадей соответствующих треугольников, равен:
\(\frac{\Delta MNP}{\Delta ABC} = \frac{2}{3}\)
Для вычисления площади треугольника MNP будем использовать формулу площади через две стороны и угол между ними:
\(S_{MNP} = \frac{1}{2} \cdot MN \cdot NP \cdot \sin \angle MNP\)
Где:
\(MN = \frac{AB}{3}\) — так как треугольники подобны, сторона MN равна одной трети стороны AB
\(NP = \frac{BC}{3}\) — аналогично, сторона NP равна одной трети стороны BC
\(\angle MNP = \angle ABC\) — так как треугольники подобны, углы между соответствующими сторонами равны
Подставляя эти значения в формулу, получаем:
\(S_{MNP} = \frac{1}{2} \cdot \frac{AB}{3} \cdot \frac{BC}{3} \cdot \sin \angle ABC\)
\(S_{MNP} = \frac{ABC}{9} \cdot \sin \angle ABC\)
\(S_{MNP} = \frac{40}{9} \text{ см}^2\)
Таким образом, окончательный ответ можно записать в виде смешанной дроби:
\(4\frac{4}{9} \text{ см}^2\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!