ГДЗ по Геометрии 10 класс Номер 102 Атанасян — Подробные Ответы

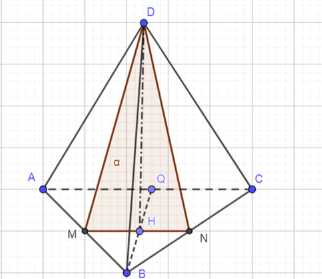
Докажите, что плоскость о, проходящая через середины двух рёбер основания тетраэдра и вершину, не принадлежащую основанию, параллельна третьему ребру основания. Найдите периметр и площадь сечения тетраэдра плоскостью и, если длины всех рёбер тетраэдра равны 20 см.

Дано: ΔABC — тетраэдр; M, N — середины AB и BC соответственно; a ∈ MND; AB = BC = AC = DA = DB = DC = 20 см.

Доказать: a || AC.
Найти: PMDN, SMDN.

Доказательство a || AC:
Так как MN — средняя линия ΔABC, то MN || AC (по теореме о средней линии). Также MN ∈ a, AC ⊥ a (по свойству средней линии). Следовательно, a || AC (по теореме о параллельности).

Вычисление PMDN:
Так как все грани ΔABC — правильные треугольники, то DN = DM — медианы и высоты этих треугольников.
PMDN = 2DN + MN
MN = 10 см (как средняя линия)
DN = \(\sqrt{3}\) · DC = 10\(\sqrt{3}\) см (так как все стороны равны 20 см)
Тогда PMDN = 2 · 10\(\sqrt{3}\) + 10 = 10(2\(\sqrt{3}\) + 1) см

Вычисление SMDN:
SMDN = \(\frac{1}{2}\) · DH · MN
ΔMDN — равнобедренный, значит DH — высота, медиана и биссектриса, перпендикулярная MN
NH = \(\frac{1}{2}\) · MN = 5 см
DH^2 = DN^2 — NH^2 = (10\(\sqrt{3}\))^2 — 5^2 = 300 — 25 = 275
DH = \(\sqrt{275}\) = 5\(\sqrt{11}\) см
SMDN = \(\frac{1}{2}\) · 5\(\sqrt{11}\) · 10 = 25\(\sqrt{11}\) см²

Ответ:
PMDN = 10(2\(\sqrt{3}\) + 1) см
SMDN = 25\(\sqrt{11}\) см²

Дано: ΔABC — тетраэдр; M, N — середины AB и BC соответственно; a ∈ MND; AB = BC = AC = DA = DB = DC = 20 см.

Доказать: a || AC.
Найти: PMDN, SMDN.

Доказательство a || AC:
1. Так как ΔABC — тетраэдр, то его грани являются правильными треугольниками.
2. По теореме о средней линии в треугольнике, средняя линия MN параллельна основанию AC: MN || AC.
3. Также известно, что прямая a проходит через середину MN отрезка BC.
4. Так как MN || AC и a ∈ MND, то a || AC (по теореме о параллельных прямых).

Вычисление PMDN:
1. Так как все грани ΔABC — правильные треугольники, то DN = DM — медианы и высоты этих треугольников.
2. PMDN = 2DN + MN
3. MN = 10 см (как средняя линия)
4. DN = \(\sqrt{3}\) · DC = 10\(\sqrt{3}\) см (так как все стороны равны 20 см)
5. Тогда PMDN = 2 · 10\(\sqrt{3}\) + 10 = 10(2\(\sqrt{3}\) + 1) см

Вычисление SMDN:
1. SMDN = \(\frac{1}{2}\) · DH · MN
2. ΔMDN — равнобедренный, значит DH — высота, медиана и биссектриса, перпендикулярная MN
3. NH = \(\frac{1}{2}\) · MN = 5 см
4. DH^2 = DN^2 — NH^2 = (10\(\sqrt{3}\))^2 — 5^2 = 300 — 25 = 275
5. DH = \(\sqrt{275}\) = 5\(\sqrt{11}\) см
6. SMDN = \(\frac{1}{2}\) · 5\(\sqrt{11}\) · 10 = 25\(\sqrt{11}\) см²

Ответ:
PMDN = 10(2\(\sqrt{3}\) + 1) см
SMDN = 25\(\sqrt{11}\) см²