
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 101 Атанасян — Подробные Ответы
Докажите, что отрезки, соединяющие середины противоположных рёбер тетраэдра, пересекаются и точкой пересечения делятся пополам.
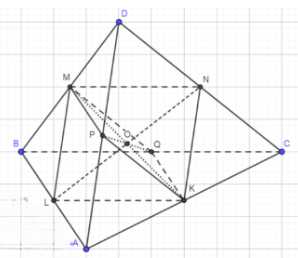
Докажем, что отрезки, соединяющие середины противоположных рёбер тетраэдра, пересекаются и делятся пополам. Рассмотрим четырехугольник MNKL, образованный серединами четырех ребер тетраэдра. Так как \(MN = \frac{1}{2}BC = LK\) (свойство средней линии треугольника), MNKL является параллелограммом, а его диагонали пересекаются в одной точке O и делятся пополам. Аналогично, четырехугольник MPKQ, образованный серединами других четырех ребер тетраэдра, также является параллелограммом, а его диагонали пересекаются в одной точке O1 и делятся пополам. Так как точки O и O1 совпадают, отрезки, соединяющие середины противоположных ребер тетраэдра, пересекаются в одной точке и делятся ею пополам.
Для доказательства того, что отрезки, соединяющие середины противоположных рёбер тетраэдра, пересекаются и делятся пополам, рассмотрим следующие шаги:
1. Рассмотрим четырехугольник MNKL, образованный серединами четырех ребер тетраэдра. Докажем, что этот четырехугольник является параллелограммом.
— Так как MN, BC и LK являются средними линиями треугольников, то \(MN = \frac{1}{2}BC = LK\) (свойство средней линии треугольника).
— Следовательно, MNKL является параллелограммом, так как противоположные стороны равны.
— Кроме того, диагонали параллелограмма пересекаются в одной точке O и делятся пополам.
2. Рассмотрим четырехугольник MPKQ, образованный серединами других четырех ребер тетраэдра. Докажем, что этот четырехугольник также является параллелограммом.
— Аналогично первому случаю, \(MP = \frac{1}{2}AB = KQ\) (свойство средней линии треугольника).
— Следовательно, MPKQ является параллелограммом, а его диагонали пересекаются в одной точке O1 и делятся пополам.
3. Так как точки O и O1 совпадают, то отрезки, соединяющие середины противоположных ребер тетраэдра, пересекаются в одной точке и делятся ею пополам.
Таким образом, мы доказали, что отрезки, соединяющие середины противоположных ребер тетраэдра, пересекаются в одной точке и делятся ею пополам.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!