Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 10 Атанасян — Подробные Ответы
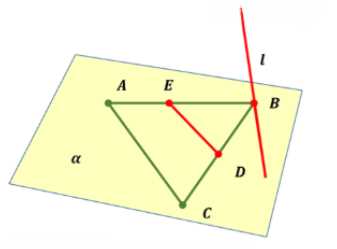
Верно ли, что прямая лежит в плоскости данного треугольника, если она: а) пересекает две стороны треугольника; б) проходит через одну из вершин треугольника?
Дано: \(ABC\) — треугольник, \(E \in [AB]\), \(D \in [BC]\), \(E, D \in \ell\).
а) Так как \(E \in [AB]\) и \(D \in [BC]\), а \(AB \subset \alpha\), \(BC \subset \alpha\), то \(E, D \in \alpha\). Следовательно, \(ED \subset \alpha\).
б) Прямая \(\ell\) не лежит в \(\alpha\), так как она пересекает плоскость \(\alpha\) только в двух точках \(E\) и \(D\).
Ответ: а) да, \(ED \subset \alpha\), б) нет, \(\ell \not\subset \alpha\).
Дано: \(ABC\) — треугольник, \(E \in [AB]\), \(D \in [BC]\), \(E, D \in \ell\). Нужно выяснить: а) \(ED \subset \alpha\)? б) \(\ell \subset \alpha\)? Где \(\alpha\) — плоскость треугольника \(ABC\).
Рассмотрим пункт а). Так как \(AB \subset \alpha\) и \(E \in [AB]\), то \(E \in \alpha\). Аналогично, так как \(BC \subset \alpha\) и \(D \in [BC]\), то \(D \in \alpha\). По аксиоме принадлежности плоскости, если две точки прямой принадлежат плоскости, то вся прямая, проходящая через эти точки, лежит в этой плоскости. Следовательно, \(ED \subset \alpha\). Ответ: да, \(ED \subset \alpha\).
Рассмотрим пункт б). Прямая \(\ell\) лежит в плоскости \(\alpha\), если она либо полностью содержится в \(\alpha\), либо пересекает плоскость в трёх точках. Из условия известно, что \(\ell\) пересекает плоскость \(\alpha\) в двух точках \(E\) и \(D\). Однако для того, чтобы \(\ell \subset \alpha\), требуется, чтобы все точки \(\ell\) принадлежали \(\alpha\). Если \(\ell\) пересекает плоскость только в двух точках, то она не лежит в плоскости \(\alpha\). Следовательно, \(\ell \not\subset \alpha\). Ответ: нет, \(\ell \not\subset \alpha\).
Итог: а) \(ED \subset \alpha\) — верно, б) \(\ell \subset \alpha\) — неверно.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.